Sorting Algorithms : A Comprehensive Guide

Sorting Algorithms : Explained With Illustrations

Sorting is the process of structuring data in a specific format. The sorting algorithm explicitly states how to arrange data in a specific order. The most popular orders are numerical or lexicographical.

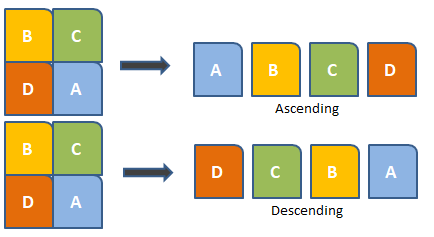
When humans understood the importance of searching speedily, they coined the term sorting. The significance of sorting stems from the fact that if data is stored in a sorted manner, data searching can be optimized to a very high level. Sorting is also used to make data more readable.

The following are a few examples of sorting in real-world scenarios.

1. Telephone Directory: The telephone directory stores people’s phone numbers alphabetically so that the names can be easily searched.

2. Dictionary: Words are stored in alphabetical order in the dictionary, making it easy to find any word.

Sorting algorithms can be classified into two types.

Integer sorts
Comparison sorts

Integer sorts

Counting sorts are another name for integer sorts (though there is a specific integer sort algorithm called counting sort). Integer sorts ascertain how many elements are less than x for each element x. If there are 14 elements that are less than x, x will be assigned to the 15th slot. This information is used to instantaneously place each element in the correct slot, eliminating the need to rearrange lists.

Comparison sorts

For each step of the algorithm, comparison sorts start comparing elements to decide whether one element should be to the left or right of another. Comparison sorts are usually simple to execute than integer sorts, but they are restricted by a lower bound of O(nlogn), which means that on average, comparison sorts cannot be speedier than O(nlogn).

In-place Sorting and Not-in-place Sorting

Sorting algorithms may necessitate additional storage for comparison and temporary storage of a few data elements. The algorithms do not require any additional space, and sorting is said to occur in-place, or even within the array itself is known as in-place sorting. In-place sorting is demonstrated by the bubble sort.

Nevertheless, in some sorting algorithms, the implementation involves space that is greater than or equal to the number of elements being sorted. Sorting that takes up equal or more space is referred to as not-in-place sorting. Not-in-place sorting is demonstrated by merge-sort.

Stable and Not Stable Sorting

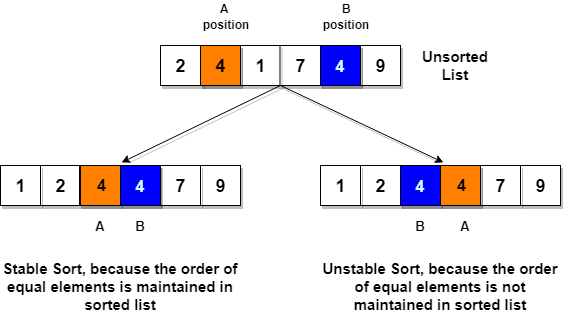
Stable sorting occurs when a sorting algorithm, after sorting the contents, does not change the pattern of similar content in which individuals exist.

Unstable sorting occurs when a sorting algorithm, after sorting the components, alters the order in which similar content initially appeared.

Adaptive and Non-Adaptive Sorting Algorithm

If a sorting algorithm takes advantage of already ‘sorted’ elements in the list to be sorted, it is said to be adaptive. That is, if an element in the source list has already been sorted, adaptive algorithms will take this into account and try not to re-order it.

A non-adaptive algorithm is one that does not take into account previously sorted elements. They attempt to force every single element to be re-ordered in order to confirm their sorting.

Sorting Efficiency

If you ask me whether I can arrange a deck of shuffled cards, I will tell you that I will begin by inspecting every card and building the deck as I go. It may take me hours to get the deck in order, but that’s how I’m going to do it. Fortunately, computers do not operate in this manner. Computer scientists have been working on solving the problem of sorting data since the dawn of the programming age, devising various algorithms to do so.

The two main criteria used to determine which algorithm is superior to the other have been :

The amount of time it took.
The use of memory space.

Different Sorting Algorithms

There are numerous sorting techniques available, each with its own set of advantages and disadvantages in terms of efficiency and space requirements. Here are some examples of popular sorting algorithms.

1 — Merge Sort

Mergesort is a comparison-based algorithm that focuses on how to merge two pre-sorted arrays into a single sorted array.

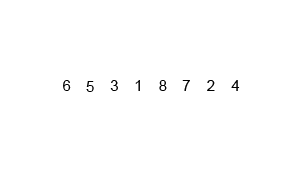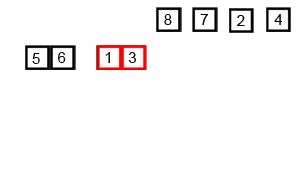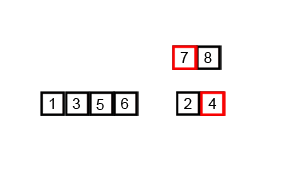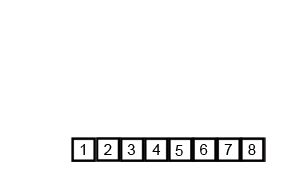
2 — Insertion Sort

Insertion sort is a comparison-based algorithm that sorts an array one element at a time. It iterates through an input array, removing one element per iteration, finding the element’s proper place in the array, and placing it there.

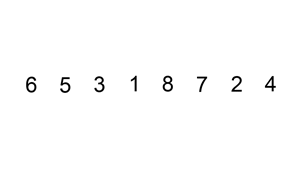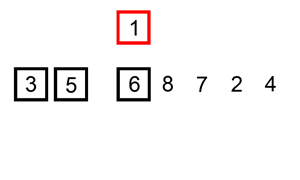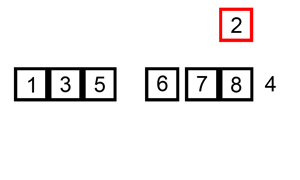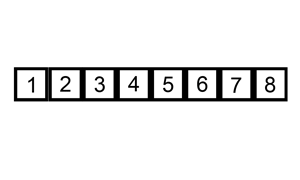
3 — Bubble Sort

Bubble sort is a comparison-based algorithm that measures up each pair of array elements and swaps them when they’re out of order until the entire array is sorted. The algorithm compares every pair of elements in the list for each element in the list.

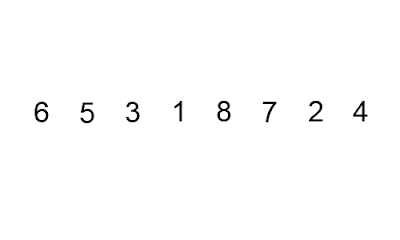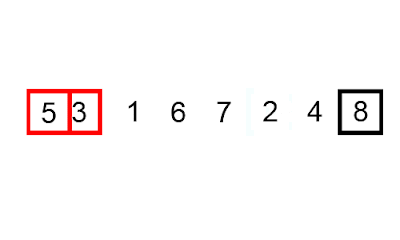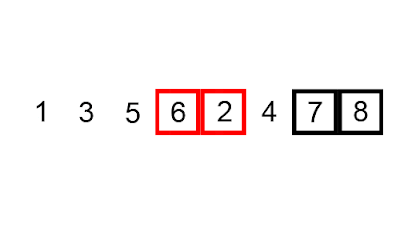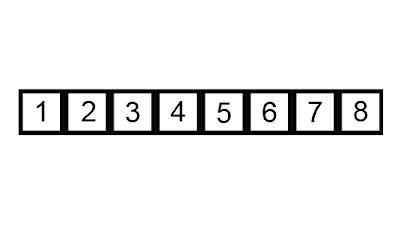
4 — Quicksort

Quicksort is a comparison-based algorithm that sorts an array using divide-and-conquer. The algorithm selects a pivot element, A[q], and then divides the array into two subarrays, A[p…q1], in which all elements are less than A[q], and A[q+1…r], in which all elements are greater than or equal to A[q].

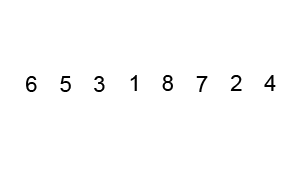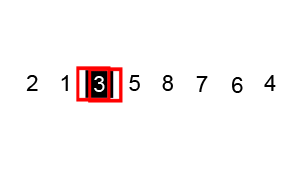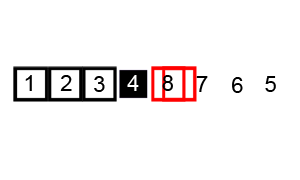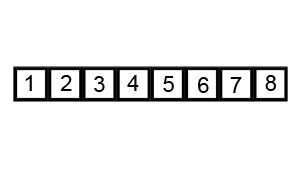
5 — Heapsort

Heapsort is a comparison-based algorithm that sorts elements using a binary heap data structure. It divides its input into a sorted and an unsorted region, then shrinks the unsorted region iteratively by extracting the largest element and moving it to the sorted region.

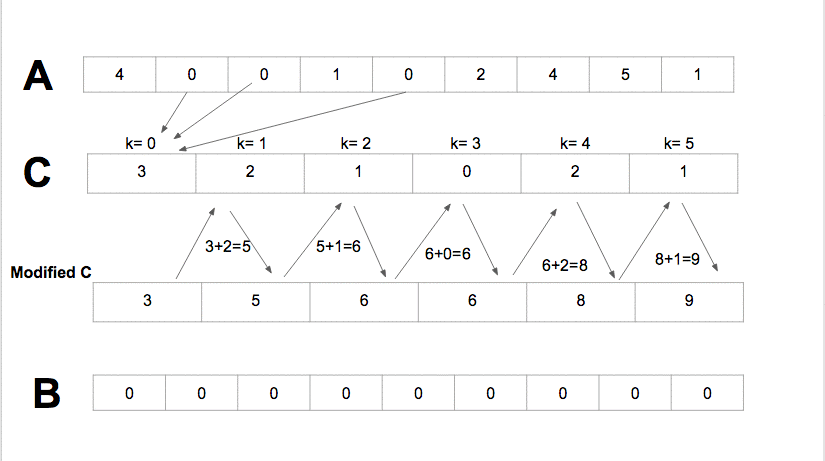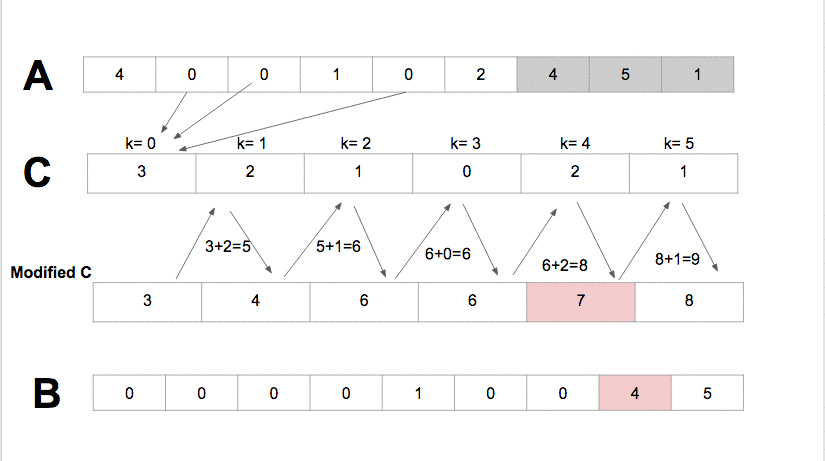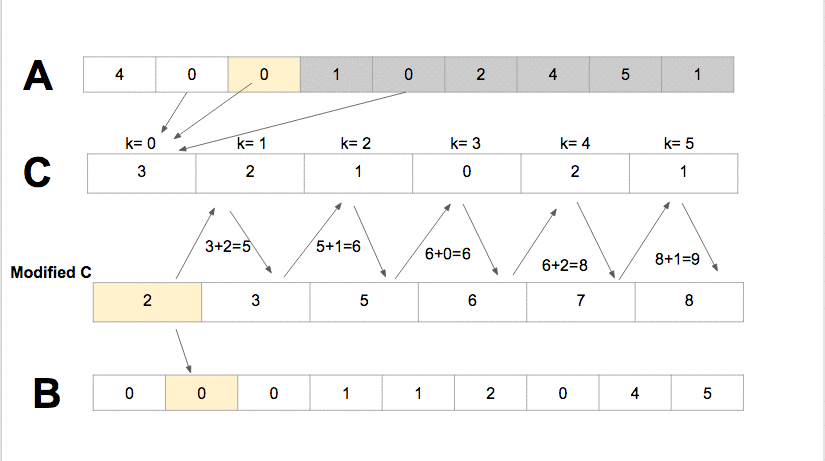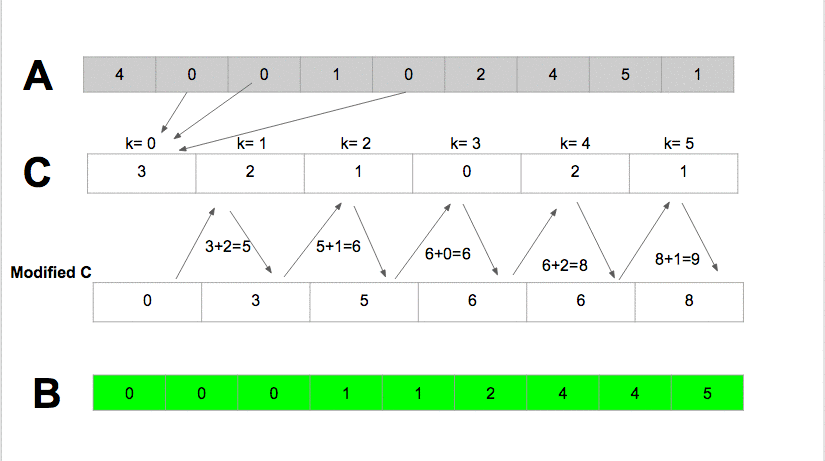
6 — Counting Sort

Counting sort is an integer sorting algorithm that supposes that for some integer k, each of the n input elements in a list has a key value ranging from 0 to k. Counting sort decides the number of elements in the list that are less than it for each element in the list. This information can be used by counting sort to place the element explicitly into the correct slot of the output array.

How to choose a Sorting Algorithm?

Consider the running time, space complexity, and expected format of the input list when selecting a sorting algorithm for a specific problem.

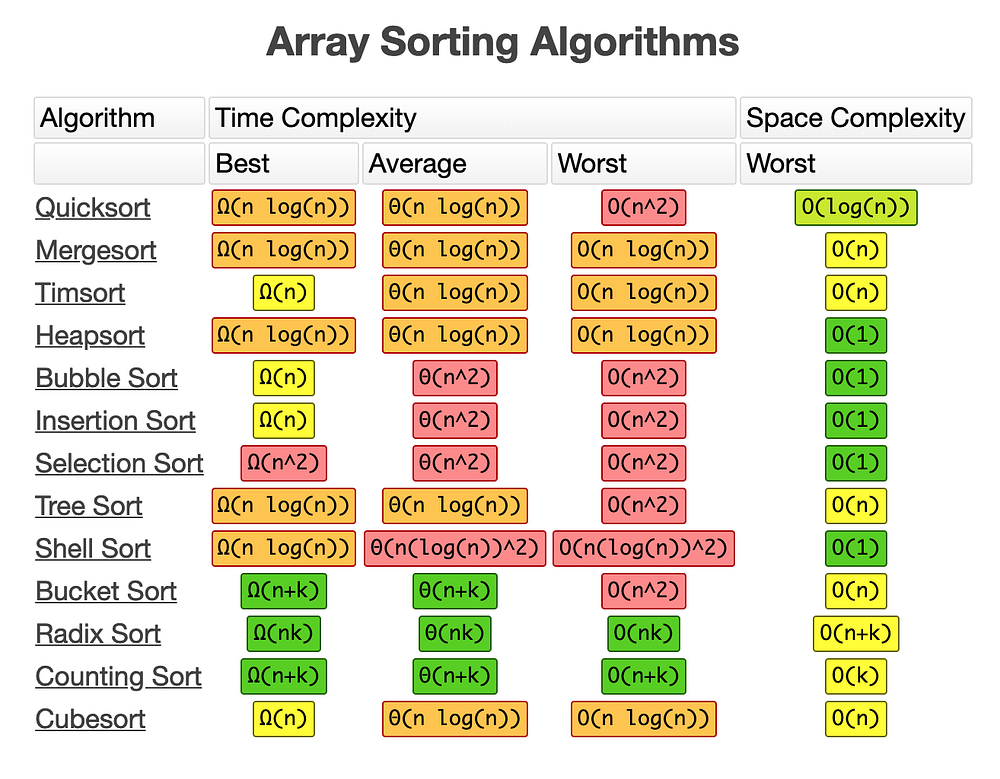
Quicksort, for example, is a fast algorithm that can be difficult to implement; bubble sort, on the other hand, is a slow algorithm that is very simple to implement. Bubble sort may be a better option for sorting small sets of data because it can be implemented quickly, but for larger datasets, the speedup from quicksort may be worth the trouble of implementing the algorithm.

Hope this can help you! Share your thoughts too.

Parallel A* Search on GPU

A* search is a fundamental topic in Artificial Intelligence. In this article, let’s see how we can implement this marvelous algorithm in parallel on Graphics Processing Unit (GPU). Traditional A* Search Classical A* search implementations typically use two lists, the open list, and the closed list, to store the states during expansion. The closed list stores all of the visited states and is used to prevent the same state from being expanded multiple times. To detect duplicated nodes, this list is frequently implemented by a linked hash table. The open list normally contains states whose successors have not yet been thoroughly investigated. The open list’s data structure is a priority queue, which is typically implemented by a binary heap. The open list of states is sorted using the heuristic function f(x) : f(x) = g(x) + h(x). The distance or cost from the starting node to the current state x is defined by the function g(x) , and the estimated distance or cost from the current stat

Decrypt Here

Search This Blog